| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- mysql
- ios
- 캡스톤정리
- Docker
- Swift
- Greedy
- C++
- NeuralNetwork
- dp
- 백트래킹
- 그래프
- 그리디
- Blockchain
- dfs
- sigmoid
- 실버쥐
- Stack
- 풀이
- 플로이드와샬
- 탐색
- Algorithm
- 알고리즘
- BFS
- Node.js
- 부르트포스
- 프로그래머스
- 백준
- 문제풀이
- ReLU
- DeepLearning
- Today
- Total
개발아 담하자
[Deep Learning] Training NeuralNetwork(2) : Weight Initialization, Batch Normalization 본문
[Deep Learning] Training NeuralNetwork(2) : Weight Initialization, Batch Normalization
choidam 2020. 5. 26. 20:591. Weight Initialization
딥러닝 학습에 있어서 초기 가중치 설정은 매우 중요한 역할을 한다.
초기값 설정을 잘못해 문제가 발생하는 경우들을 살펴보자.
문제 발생 1 : W 가 모두 같은 경우 (혹은 다 0인 경우)
만약 데이터를 평균 0으로 정규화 시킨다면, 가중치를 0으로 초기화 시킨다는 것이 합리적으로 보일 수 있다.
그러나 실제로 0으로 가중치를 초기화하면 모든 뉴런들이 같은 값을 나타낼 것이고, 역전파 과정에서 각 가중치의 update 가 동일하게 이뤄질 것이다. 결국 제대로 학습하기 어려울 것이다.
문제 발생 2 :small random number 을 줬을 경우
import numpy as np
from matplotlib.pylab import plt
# assume some unit gaussian 10-D input data
D = np.random.randn(1000, 500)
hidden_layer_sizes = [500]*10
nonlinearities = ['tanh']*len(hidden_layer_sizes)
act = {'relu': lambda x:np.maximum(0,x), 'tanh':lambda x: np.tanh(x)}
Hs = {}
for i in range(len(hidden_layer_sizes)):
X = D if i==0 else Hs[i-1] # input at this layer
fan_in = X.shape[1]
fan_out = hidden_layer_sizes[i]
W = np.random.randn(fan_in, fan_out) * 0.01 # layer initialization
H = np.dot(X, W) # matrix multiply
H = act[nonlinearities[i]](H) # nonlinearity
Hs[i] = H # cache result on this layer
print('input layer had mean', np.mean(D), 'and std', np.std(D))
# look at distributions at each layer
layer_means = [np.mean(H) for i,H in Hs.items()]
layer_stds = [np.std(H) for i,H in Hs.items()]
# print
for i,H in Hs.items() :
print('hidden layer', i+1, 'had mean', layer_means[i], 'and std', layer_stds[i])
plt.figure()
plt.subplot(1,2,1)
plt.title("layer mean")
plt.plot(range(10), layer_means, 'ob-')
plt.subplot(1,2,2)
plt.title("layer std")
plt.plot(range(10), layer_stds, 'or-')
plt.show()
plt.figure()
for i,H in Hs.items() :
plt.subplot(1,len(Hs), i+1)
plt.hist(H.ravel(), 30, range=(-1,1))
plt.show()예시 코드는 python 2 기준이라서 문법 몇 부분을 수정했다..
input layer had mean 0.00031233516316648657 and std 1.0006710331935624
hidden layer 1 had mean 0.0032899684992063636 and std 0.9820452751182597
hidden layer 2 had mean 0.003931758696050947 and std 0.9819251097074527
hidden layer 3 had mean 0.0026063736923909596 and std 0.9817340581953854
hidden layer 4 had mean 0.001848042971495998 and std 0.9817977909967206
hidden layer 5 had mean -0.0016554517737738606 and std 0.9815496358911521
hidden layer 6 had mean 0.0006604474921595372 and std 0.9816919440654884
hidden layer 7 had mean 0.0001594571291677151 and std 0.9816941165792189
hidden layer 8 had mean -0.0011475135707183642 and std 0.9816304323127083
hidden layer 9 had mean 0.0018214029856872354 and std 0.9815362486244705
hidden layer 10 had mean -0.0013684972820372828 and std 0.981809472200405

처음 layer에는 정규 분포가 잘 이루어지지만 layer가 쌓일 수록 0에 뭉친다.
x가 0에 가까워지면 gradient도 0에 가까워져서 Vanishing gradient 가 발생한다.
문제 발생 3. 2의 case 에서 0.01 대신 1을 곱했을 경우
W = np.random.randn(fan_in, fan_out) * 1.0 # layer initializationinput layer had mean -0.0004322766817344249 and std 1.0010016502837895
hidden layer 1 had mean -0.0012174416683021685 and std 0.981880039850602
hidden layer 2 had mean -0.0015410543140147272 and std 0.9814327560617824
hidden layer 3 had mean -0.00031650342142403704 and std 0.9817555532084202
hidden layer 4 had mean -0.002599692767592639 and std 0.9817765320254677
hidden layer 5 had mean 0.00021900665038415243 and std 0.9816731709326508
hidden layer 6 had mean 0.0027174686541096625 and std 0.9817325832571894
hidden layer 7 had mean 0.00035636251219643234 and std 0.9817815950648252
hidden layer 8 had mean -0.0015383316857630897 and std 0.9817278825435273
hidden layer 9 had mean -0.00048497563819457115 and std 0.9817507524970054
hidden layer 10 had mean 0.0015641156086318114 and std 0.9818682873635451

Gradient가 0이 되어학습이 진행되지 않는다. 값이 너무 클 경우 분포가 양쪽으로 튄다.
위 문제들을 해결하기 위한 알맞게 가중치를 초기화하는 방법에 대해 알아보자
초기화 1 :Xavier Initialization
W = np.random.randn(fan_in, fan_out) / np.sqrt(fan_in)Xavier 초기화 방법은 표준 정규 분포를 입력 개수의 표준 편차로 나누는 방법이다.
input layer had mean -0.0007602850190879709 and std 0.9998665656626502
hidden layer 1 had mean 0.0002708052235341852 and std 0.6286386350311198
hidden layer 2 had mean 7.981811704091712e-05 and std 0.4871593737123403
hidden layer 3 had mean -5.8048525414097e-05 and std 0.4095861395151598
hidden layer 4 had mean -0.0003551174024725932 and std 0.35836212510095666
hidden layer 5 had mean -0.0005494540483613055 and std 0.32226268320263796
hidden layer 6 had mean -0.0009404907509430189 and std 0.2955054628386911
hidden layer 7 had mean -0.00031023383926448016 and std 0.27523767970783497
hidden layer 8 had mean -0.00033325822421282486 and std 0.25767757148442433
hidden layer 9 had mean -0.0006399647322567711 and std 0.24192558051206042
hidden layer 10 had mean 0.00011454739685321903 and std 0.22988941690330594

이전 노드와 다음 노드의 개수에 의존하는 방법이다.
Gradient Vanishing 현상을 완화하기 위해서 가중치를 초기화 할 때 sigmoid 와 같은 s 자 함수의 경우 가장 중요한 것은 출력값들이 표준 정규 분포 형태를 갖게 하는 것이다. 출력값들이 표준 정규 분포 형태를 갖게 되어야 안정적으로 학습이 가능하기 때문이다.
Xavier 함수는 비선형 함수 (sigmoid, tanh) 에서 효과적인 결과를 보여준다.
nonlinearities = ['relu']*len(hidden_layer_sizes) W = np.random.randn(fan_in, fan_out) / np.sqrt(fan_in)

Xavier 초기화 방법과 ReLU 함수를 결합했을 때 그래프이다. 출력값, 평균, 표준편차 모두 0으로 수렴한다. 그러므로 ReLU 함수를 사용할 경우에는 Xavier 초기화 방법을 사용할 수 없다.
초기화 2: He Initialization
W = np.random.randn(fan_in, fan_out) / np.sqrt(2/fan_in)

He 초기화와 ReLU 함수를 사용했을 때의 그래프이다. 10층 layer에서도 평균과 표준편차가 모두 0으로 수렴하지 않는다.
conclusion on Weight Initialization
- sigmoid, tanh : use Xavier
- ReLU : use He
Batch Normalization
배치 정규화 는 Activation Function 의 활성화값 또는 출력값을 정규화 (정규 분포로 만듦) 하는 작업을 말한다.
신경망을 학습시킬 때 보통 전체 데이터를 한 번에 학습시키지 않고 조그만 단위로 분할해서 학습을 시키는 데 이 때 조그만 단위가 배치다.
신경망의 각 layer 에서 데이터 (배치) 의 분포를 정규화 하는 작업이다.
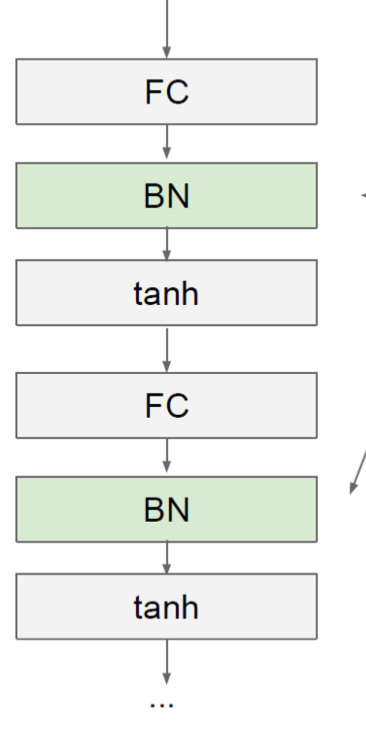
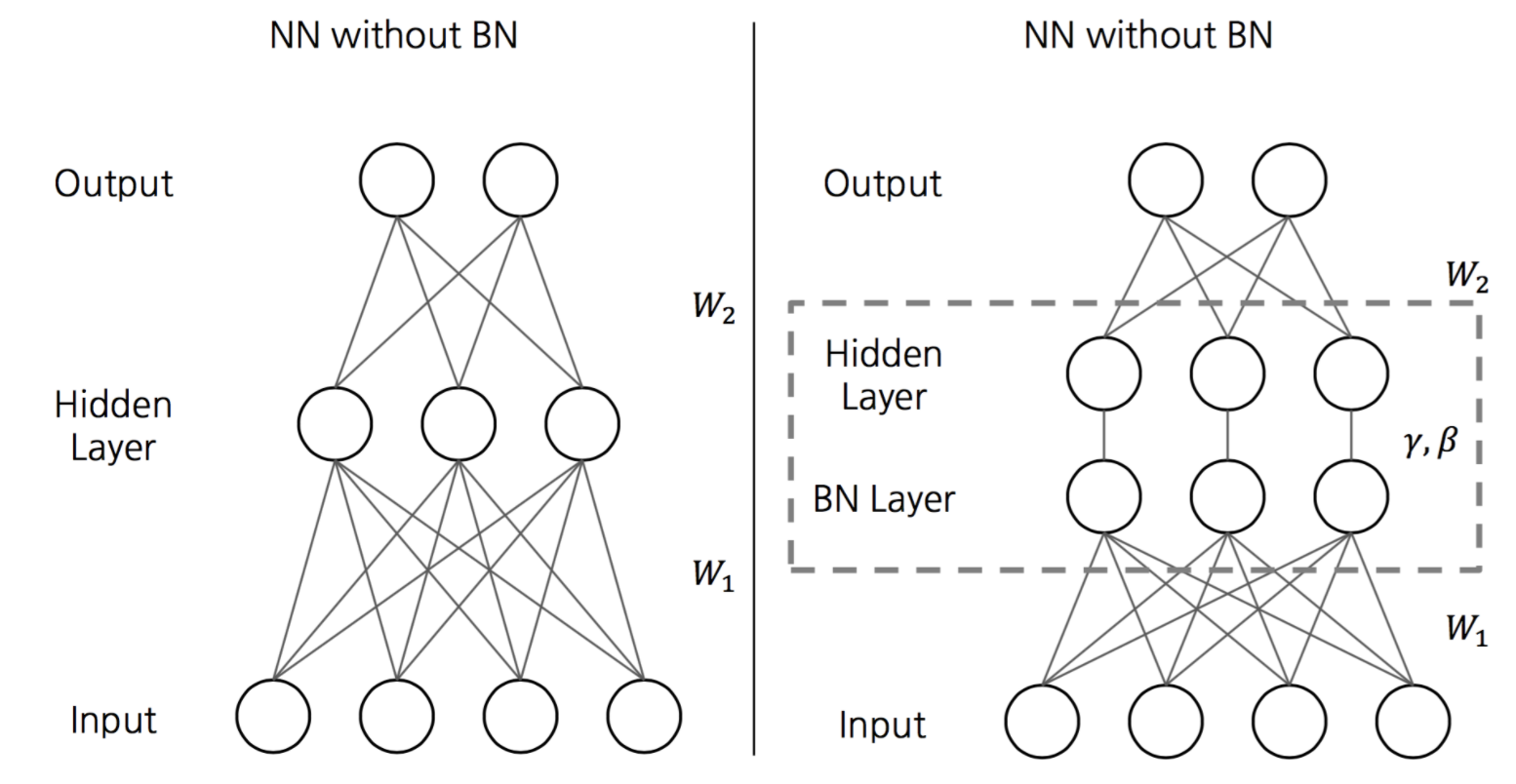
깊은 신경망일 수록 같은 Input 값을 갖더라도 가중치가 조금만 달라지면 완전히 다른 값을 얻을 수 있다. 이를 해결하기 위해 각 층의 출력값에 배치 정규화 과정을 추가해준다면 가중치의 차이를 완화하여 보다 안정적인 학습이 이루어질 수 있다.
입력 분포가 일정하게 되어 Learning rate 를 크게 설정해도 괜찮아진다.

출력값을 정규화 할 때 평균, 표준편차, 얼마나 이동시킬지 등의 parameter 들 또한 역전파를 통해 학습이 가능하다.
Gamma 와 Beta 를 학습하도록 하면 Normalize 효과를 어느정도 적용할 지 적용이 가능하다.
Conclusion on Batch Normalization
학습 속도가 개선된다. (학습률을 높게 설정할 수 있기 때문)
가중치 초깃값 선택의 의존성이 적어진다. (학습을 할 때마다 출력값을 정규화하기 때문)
overfitting (과적합) 위험을 줄일 수 있다. drop out 같은 기법 대체 가능
Gradient Vanishing 문제 해결이 가능하다.
그러니까 🔥 사용하는게 좋다 🔥
Summary ✍️
- Activation Function : use ReLU
- Data preprocessing: subtract mean
- Weight Initialization: use Xavier or He
- Batch Normalization : use
- Babysitting the learning process
- Hyperparameter optimization : random sample hyperparams 👉 grid
'🚀 Deep Learning' 카테고리의 다른 글
| [Deep Learning] Text and Sequences (0) | 2020.06.26 |
|---|---|
| [Deep Learning] Training NeuralNetwork(3) : Optimization (2) | 2020.05.26 |
| [Deep Learning] Training NeuralNetwork(1) : Activation Function (0) | 2020.05.03 |
| [Deep Learning] Back Propagation 구현하기 (1) | 2020.05.03 |
| [Deep Learning] Gradient Descent 란 ? (0) | 2020.04.24 |




