| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 알고리즘
- dp
- NeuralNetwork
- Docker
- 풀이
- 플로이드와샬
- Stack
- DeepLearning
- 캡스톤정리
- Swift
- sigmoid
- 백트래킹
- ios
- Greedy
- BFS
- 그래프
- ReLU
- 실버쥐
- dfs
- 부르트포스
- 백준
- Blockchain
- 그리디
- 문제풀이
- Algorithm
- mysql
- 탐색
- 프로그래머스
- C++
- Node.js
- Today
- Total
개발아 담하자
[Deep Learning] Training NeuralNetwork(3) : Optimization 본문
Optimization
딥러닝에서 optimization 은 학습속도를 안정적이게 하는 것을 의미한다.


위 optimizer들에 대해 자세히 살펴보자.
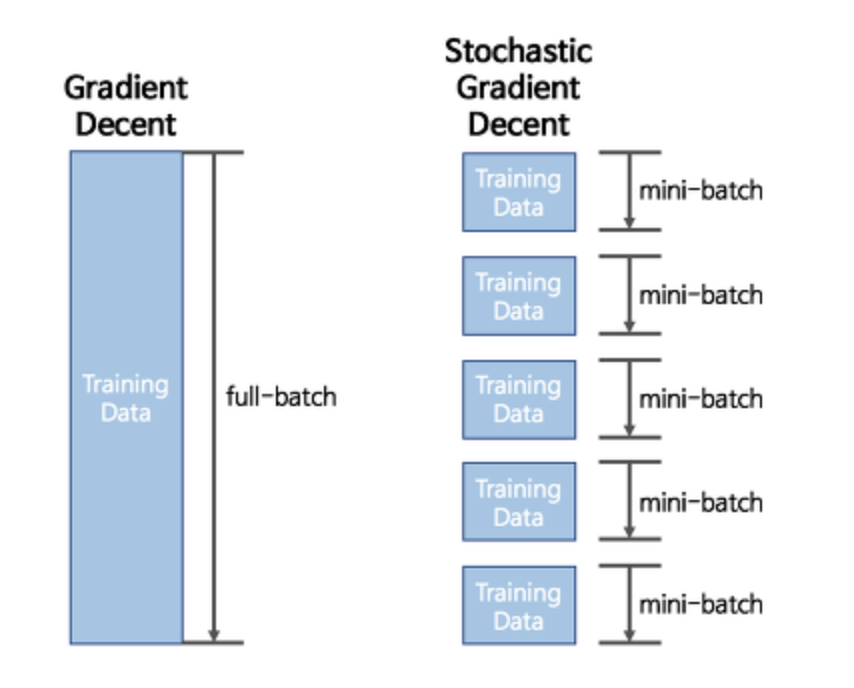
1. SGD (Stochastic gradient descent)
Gradient Descent 는 전체 dataset 을 가지고 한 발자국 전진할 때마다 (learning rate) 최적의 값을 찾아 나간다.
그러나 SGD는 Mini-batch 사이즈 만큼 조금씩 돌려서 최적의 값으로 찾아간다.
이 방법은 GD 보다 다소 부정확할 수는 있지만, 훨씬 계산 속도가 빠르기 때문에 같은 시간에 더 많은 step 을 갈 수 있으며, 여러 번 반복할 경우 보통 batch 의 결과와 유사한 결과로 수렴한다. 또한, GD 에서 빠질 local minima 에 빠지지 않고 더 좋은 방향으로 수렴할 가능성도 있다.
import numpy as np
class Optimizer:
def __init__(self, learning_rate=0.01):
self.lr = learning_rate
def update(self, weight, grad):
weight
""" Stochastic gradient descent """
class SGD(Optimizer):
def __init__(self, learning_rate=0.01):
super().__init__(learning_rate)
def update(self, weight, grad):
weight -= self.lr * grad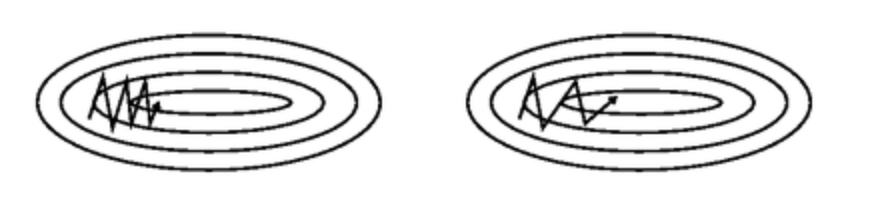
그러나 문제점이 존재한다. mini batch 를 통해 학습시키는 경우 최적의 값을 찾아 가기 위한 방향 설정이 뒤죽박죽이기 때문이다.
2. Momentum
momentum 은 누적된 과거 gradient 가 지향하고 있는 방향을 현재 gradient 에 보정하는 방식이다.
기울기 업데이트 시 폭을 조절하는 역할을 하며 이에 따라 velocity 가 변한다.
class Momentum(Optimizer):
def __init__(self, learning_rate=0.01, momentum=0.9):
super().__init__(learning_rate)
self.momentum = momentum
self.v = None
def update(self, weight, grad):
if self.v is None:
self.v = np.zeros_like(weight)
self.v = self.momentum * self.v - self.lr * grad
weight += self.v
3. NAG (Nestrov Accelerated Gradient)

momentum 은 이동 벡터를 계산할 때 현재 위치에서의 gradient 와 momentum step 을 독립적으로 계산하고 합친다.
반면 NAG 에서는 momentum step을 먼저 이동했다고 생각한 후 그 자리에서의 gradient 를 구해서 gradient step 을 이동한다.
momentum 방식의 따른 이동에 대한 이점은 누리면서도, 멈춰야 할 적절한 시점에 제동을 거는 데에 매우 용이하다.
4. AdaGrad (Adaptive Gradient Algorithm)
Adagrad 는 변수들을 update 할 때 각각의 변수마다 step size 를 다르게 설정해서 이동하는 방식이다.
즉, 자주 등장하거나 변화를 많이 한 변수들의 경우 optimum 에 가까이 있을 확률이 높기 때문에 작은 크기로 이동하면서 세밀한 값을 조정하고, 적게 변화한 변수들은 optimum 에 도달하기 위해 많이 이동해야 할 확률이 높기 때문에 먼저 빠르게 loss 값을 줄이는 방향으로 이동하는 방식이다.
class AdaGrad(Optimizer):
def __init__(self, learning_rate=0.01):
super().__init__(learning_rate)
self.cache = None # 각 차원의 gradient 가 cache에 누적됨
def update(self, weight, grad):
if self.cache is None:
self.cache = np.zeros_like(weight)
self.cache += grad ** 2
weight -= self.lr * grad / (np.sqrt(self.cache) + 1e-7)AdaGrad 를 사용하면 step size decay 를 신경쓰지 않아도 된다는 장점이 있다.
그러나, AdaGrad 로 학습을 오래 진행할 경우 step size 가 너무 적어져서 결국 거의 움직이지 않게 된다.
5. RMSProp (Root Mean Square Propagation)
AdaGrad 단점을 해결하기 위한 방법이다.
class RMSProp(Optimizer):
def __init__(self, learning_rate=0.01, decay_rate=0.9):
super().__init__(learning_rate)
self.decay_rate = decay_rate
self.cache = None
def update(self, weight, grad):
if self.cache is None:
self.cache = np.zeros_like(weight)
self.cache = self.decay_rate * self.cache + (1 - self.decay_rate) * (grad ** 2)
weight -= self.lr * grad / (np.sqrt(self.cache) + 1e-7) # AdaGrad 의 변수 update
self.cache += grad ** 2
weight -= self.lr * grad / (np.sqrt(self.cache) + 1e-7) # RMSProp 의 변수 update
self.cache = self.decay_rate * self.cache + (1 - self.decay_rate) * (grad ** 2)
weight -= self.lr * grad / (np.sqrt(self.cache) + 1e-7)AdaGrad 식에서 gradient 제곱값을 더해나가면서 구한 부분을 지수 평균으로 바꾸어 대체한 방법이다. G가 무한정 커지지 않으면서 최근 변화량의 변수 간 상대적인 크기 차이를 유지할 수 있다.
6. Adam (Adaptive Moment Estimation)
기본 idea : RMSProp + Momentum
class Adam(Optimizer):
def __init__(self, learning_rate=0.001, beta1=0.9, beta2=0.999):
super().__init__(learning_rate)
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None # 기울기의 지수 평균 (momentum)
self.v = None # 기울기 제곱값의 지수 평균 (RMSProp)
def update(self, weight, grad):
if self.m is None:
self.m = np.zeros_like(weight)
self.v = np.zeros_like(weight)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)
self.m += (1 - self.beta1) * (grad - self.m)
self.v += (1 - self.beta2) * (grad ** 2 - self.v)
weight -= lr_t * self.m / (np.sqrt(self.v) + 1e-7)Adam 에서는 m과 v가 처음에 0으로 초기화되어 있기 때문에 학습의 초반부에서는 0에 가깝게 bias 되어있을 것이라고 판단하여 이를 unbiased 하게 만들어주는 작업을 거친다.
'🚀 Deep Learning' 카테고리의 다른 글
| [Deep Learning] Text and Sequences (0) | 2020.06.26 |
|---|---|
| [Deep Learning] Training NeuralNetwork(2) : Weight Initialization, Batch Normalization (0) | 2020.05.26 |
| [Deep Learning] Training NeuralNetwork(1) : Activation Function (0) | 2020.05.03 |
| [Deep Learning] Back Propagation 구현하기 (1) | 2020.05.03 |
| [Deep Learning] Gradient Descent 란 ? (0) | 2020.04.24 |




